APPENDIX E Meaning of Item Clusters

The basic data of cluster analyses are correlation coefficients;1 in the case of the cluster analysis reported in Chapter IV, these are tetrachoric correlations between items.2

It is obviously possible that neighborhoods differ in the ways responses to the items are correlated, and this independently of whether they differ in the distributions of responses to the items individually. That is, it is possible that certain information is more closely linked to certain attitudes in one neighborhood than in another, that the possession of one bit of information is more closely linked to the possession of another in one neighborhood than it irs, in a second, or that one attitude is more closely linked to another attitude in one neighborhood than in the second.

In line with this reasoning, we computed all the correlations among items, separately for each neighborhood. With seventy-two items, however, we get 2,556 correlation coefficients, and this for each of the three neighborhoods, or a grand total of 7,668 correlation coefficients. It would obviously be an impossibly tedious job to attempt to discuss all of them, to say nothing of the imposition on the reader.

We could, of course, compromise by selecting the most interesting correlations to discuss. But, not only is it not entirely clear what the criteria for "most interesting" should be, there is also a more fundamental difficulty. The ambiguities of interpreting the meaning of a response also affect the interpretation of a correlation coefficient.3

The recognition of the ambiguity of a correlation coefficient with respect to the relationship between the two variables should, nevertheless, not blind us to the fact that two relatively highly correlated variables are, in some sense, akin. Similarly, we may note that a low correlation between two variables does not necessarily mean that there is no relationship between them. Thus, one item may be fundamentally akin to another, but undetected ambiguities in its wording may introduce a random element in the distribution of responses to it; the random element would, of course, lower the correlation and thereby conceal the evidence of kinship. Or the ambiguities of wording may raise an issue not systematically related to issues posed by any of the other items, but which nevertheless determines the responses of a sizable number of subjects. The effect may be to conceal the fact that the remaining subjects do respond to the item in a way that makes it akin to other items and the possibility that even the subjects who respond to the extraneous issues might have responded in the same way if the extraneous issue had been eliminated.

For instance, highly sophisticated subjects might well get lost in the issue of whether "take the cure" is intended to mean "merely go for detoxification" or "voluntarily continue over a long period in an intensive psychotherapeutic relationship," whereas the naïve subject would presumably respond to the phrase, with no special thought or verbalization of the meaning, in the sense that we intended, viz., "receive the commonly available form of treatment." In the distribution of responses to the item, we could have inextricably mingled at least four distinct groups of subjects: the naïve subjects, the sophisticates who arbitrarily decide that "take the cure" means one thing, the sophisticates who arbitrarily decide that it means another, and the sophisticates who decide that they do not know how to answer. The correlations of responses to this item with those to other items may well be of opposite sign in one group of sophisticates than it is in the others. The over-all correlations could thus be lowered by an essentially arbitrary decision on an extraneous issue.

We may sometimes be interested in tracing the precise nature of a relationship, and it is possible to design studies to do so. At other times, however, we may be interested in the mere fact of kinship without being concerned with the precise nature of the relationship. This is the case in the present study. We are concerned with the cultural climates in which drug use does or does not abound, rather than with the precise nature of the influences which bring the various aspects of a particular climate into a common one. Nor, for that matter, are we concerned with the precise degree of kinship between any two elements of a given climate; we want to get an over-all picture of the climate. For this purpose, it seems inappropriate to focus on the degrees of correlation among all or some of the pairs of items. What we really want to discern are the kinship groupings, the families, the sets of items that evoke responses that tend to hang together.

How can we establish these kinship groupings, or sets of items, from the correlation coefficients? The most obvious stratagem is to select sets of variables with relatively high average intercorrelations, but this procedure would not detect the kinships that might be concealed behind low correlations. We therefore used a more complicated procedure. Let us for the moment pursue the analogy of a family group. Not only does such a group include individuals only indirectly related to one another (e.g., the wife's mother and the husband's mother), but, in addition, even intimate kin may grow apart, so that the relationship is apparent only in certain conditions. The second of these considerations concerns us more than the first. That is, we are not particularly concerned whether the basis of relationship which puts items into the same kinship group is indirect. But we are concerned that the fact of relationship, whether direct or indirect, be more than historical; we want to be certain that the relationship is a continuing one, evident when the "parties" involved are examined in a wide variety of contexts.

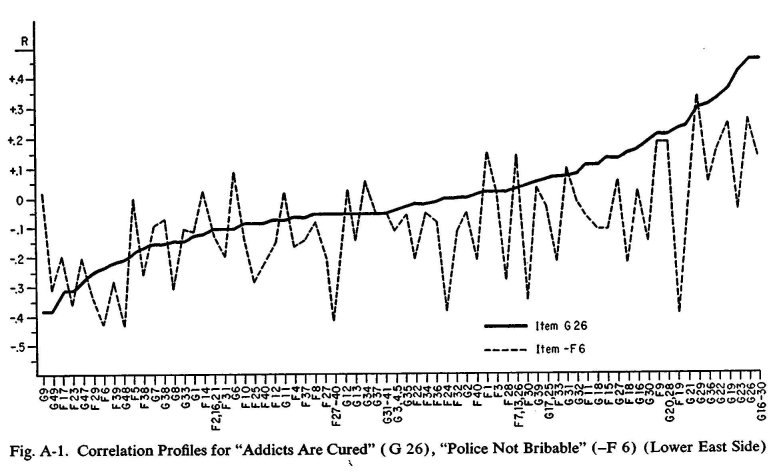
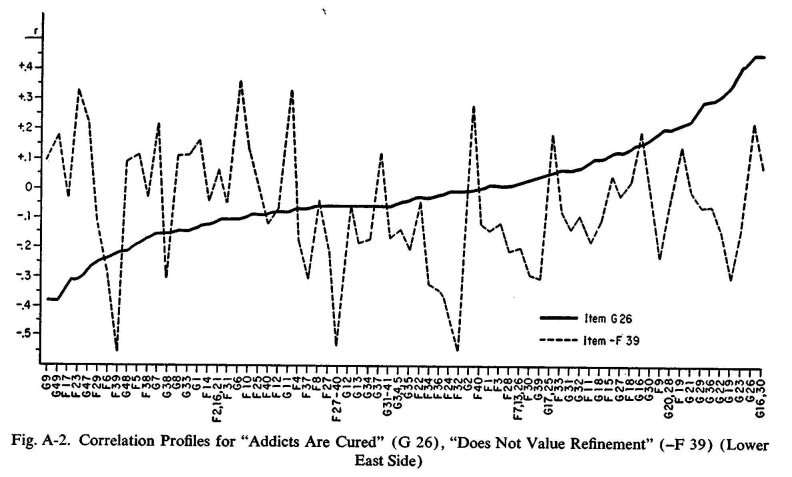
To illustrate the point, let us consider the item on cure of addiction. The correlations in one of our neighborhoods between this item and all of the other items are shown graphically in the solid line in figures A-1 and A-2. Thus, this item correlates .35 with Item G 19, .12 with Item G 27, .23 with Item G 21, and so on. Such a graphic representation of the correlation of one variable with a whole series of other variables is known as a correlation profile. The broken line in Figure A-1 is the correlation profile of the item calling for agreement or disagreement with the statement: "Most policemen can be paid off." The broken line in Figure A-2 is the correlation profile of the item calling for a "yes" or "no" to the question: "Do you want this muck more than almost anything else in the world: to have good taste—to be a person who can enjoy good art, good music, and the finer things of life?" Each of these items has almost exactly the same degree of correlation with the addiction-cure item—fairly low, but nevertheless definite. That is, by the test of direct correlation, there is a slight degree of kinship between the belief that addiction is usually permanently cured and the rejection of the idea of the venality of the police and the same slight degree of kinship between the belief in curability and the unwillingness to accept "refinement" as one of the greatest values in life.

But look at the two pairs of profiles. Obviously, the first two are much more alike than the second. That is, the degree of relationship, or lack of relationship, of the addiction-cure item to the numerous other items tends to be paralleled by the police-venality item, but not by the value-of-refinement item. Thus, although both of the latter items are directly related to the addiction-cure item to the same degree, the police-venality item shows similar relationships and lack of relationships, whereas the value-of-refinement item does not. In this extended sense, the members of the first pair are much more akin than are the members of the second; they function much more consistently as members of the same family.

We may also consider the issue in more sober statistical, and less metaphorical, terms. The demonstration of greater-than-zero correlation between two items implies that, knowing the response to one, we can make a betterthan-chance prediction of the response to the other. With two-valued variables and greater-than-zero correlation, the predicted response to one item from a high-scoring response to the other would always4 be a high-scoring response if the correlation is positive or a low-scoring response if the correlation is negative, and this regardless of the size of the correlation. Similarly, from a low-scoring response on one item, we would predict a low-scoring response on the other if the correlation is positive and a high-scoring response if the correlation is negative. If the size of the correlation does not affect the nature of the prediction, however, it does affect its precision. With a perfect correlation, we would never make errors in the prediction, and, with a zero correlation, our predictions would be no better than guesswork. The closer the correlation to one, the fewer would be the errors of our predictions; the closer the correlation to zero, the greater would be the number of errors. It follows that the size of the correlation between two items tells us the degree to which the response to one is latent (i.e., contained by statistical implication) in the response to the other. From this, it follows that two items with identical correlation profiles have an identical pattern of implication; and, the more similar the correlation profiles of two items, the more similar are the patterns of implication. Thus, the more similar the correlation profiles of two items, the greater the correspondence between the implications of the responses to these items.

Conversely, suppose that we want to predict the responses to an item from the responses to all the other items. The predictions of the scores of two items with identical correlation profiles would be identical; the precision of these predictions would also be identical. Thus, the more similar the correlation profiles of two items, the greater the correspondence of the implications for these items of the responses to the remaining items. It is in these senses that items with similar correlation profiles are akin. We may say that their latencies'are alike.

The degree of kinship, in this extended sense, can be measured simply by computing the degree of correlation between the correlation profiles. We did this and then sorted the items into sets, each set consisting of items with relatively similar profiles. The items were arranged in order of the magnitude of their average tetrachoric correlations (disregarding signs) with all of the remaining items. Starting with the first item on the list, we added to it the item with the highest profile correlation5 with it. To these two items, we added the item with the highest average profile correlation with them; to the three, the item with the highest average profile correlation with them; and so on. The only restriction was that no item could be added to the set if it had a profile correlation of less than .40 or a tetrachoric correlation of less than .20 with the items already selected. We continued in this way until there were no more items that would meet these qualifications. This gave us our first "trial set."

Eliminating the items of the first trial set, we started again with the remaining item with the highest average tetrachoric correlation with all of the other items and developed a second trial set. Similarly, for a third trial set and so on until no additional sets could be found that would meet the stated qualifications.

For each item, we calculated the average profile correlation with the items of each trial set. If an item had a higher average profile correlation with a trial set other than the one in which it was included, it was moved. This process resulted in revised trial sets. Again, for each item we calculated the average profile correlation with each of the revised trial sets, and, if indicated, items were moved. The procedure was continued until no further changes were indicated. Every item was thus located in the set with which it had the highest average profile correlation (or in no set at all). Such a set we refer to as a "prime cluster."

By this procedure, it is possible for an item in one prime cluster to have as high an average profile correlation with the items in a second prime cluster as the items in the latter do with one another. This would be particularly true of items in prime clusters with very high internal average profile correlations. Thus, an item in a cluster whose items have an average profile correlation of, say, .80 with one another might have an average profile correlation of, say, .60 with the items in a second prime cluster. If the items of the latter prime cluster have an average profile correlation with one another on the order of .60, the item from the first prime cluster fits the second about as well as the items of the latter do themselves. It seems reasonable to include such an item in the second set of items, as well as in its own prime cluster. Similarly,"if the items of a prime cluster have exceptionally high profile correlations with one another, it seems reasonable to add to this set an item which has a higher average profile correlation with the items in the cluster than is characteristic of the profile correlations of items in other prime clusters with one another, even though it does not fit the prime cluster quite so well as do the items of the latter.

When the set of items in a prime cluster is thus augmented by additional items, we refer to the augmented set of items simply as a cluster.° A prime cluster is analogous to an immediate family; a cluster, to an extended family. A given item may belong to no cluster at all, to a prime cluster only, or to a prime cluster and to one or more other clusters. An item which belongs to two or more clusters may be said to share in two or more kinship groupings.

In the neighborhood for which the data of figures A-1 and A-2 are presented, the addiction-cure and police-venality items are found in a common cluster, but they do not belong to a common prime cluster. The addiction-cure and value-of-refinement items do not even belong to a common cluster.

The items in a cluster identify a current in the cultural atmosphere of a neighborhood, a current which brings the ideas, attitudes, information, and values with which the items are concerned into common contexts of meaning. This is not to imply that particular items do not retain idiosyncratic shades of meaning for particular individuals or groups; but the statistical behaviors of the items nevertheless tell us something of the properties of the world in which these individuals live.

Since, however, an item that is added to a prime cluster fits its own prime cluster better than it does another one to which it is added, it follows that there are aspects of its character that are more salient than the aspects by virtue of which it fits the latter. Hence, the items in a prime cluster are the ones that fit best together by virtue of their most outstanding characteristics. Moreover, by the procedure we have adopted, the prime cluster is the heart of any cluster, and the additional items are introduced only because they have implications resembling those already defined by the prime cluster. It follows that,the meaning of a cluster may be most evident in a scrutiny of the items in a prime cluster and that any interpretation of a cluster is apt to be aberrant if it is not consistent with the prime cluster. The augmented cluster merely furnishes additional detail to what is already latent in the prime cluster; it helps to focus and sharpen what may be perceived in the prime cluster.

1 See Appendix F for an explanation of why we did not make use of factor analysis. For more elaborate discussions of cluster analysis, see R. C. Tryon, "Identification of Social Areas by Cluster Analysis," University of California Publications in Psychology, 8 (1955), 1-100; also, more recent publications of the same author.

2 See Appendix C for an explanation of tetrachoric correlations between items.

3 See Appendix C for a discussion of the ambiguities involved in interpreting a correlation coefficient.

4 This is the strategy that would, in the long run, produce the fewest errors of prediction. To the mathematically naïve, it may seem that the predictions should be distributed in the same way as the odds go, but it can be shown that, in the long run, this strategy would produce more errors than the strategy of always predicting the most probable outcome, and this even in the case when the odds are almost equal.

5 For convenience, we refer to a correlation between two correlational profiles as a profile correlation. Profile correlations were computed on the usual Pearsonian product-moment basis, rather than as tetrachorics.

6 The number of clusters and prime clusters distinguished by this procedure involves the exercise of judgment in a search for what seems to be the most sensible construction of the data. The procedures of cluster analysis do permit more rigorously parsimonious descriptions of data which are useful for certain purposes, e.g., in mapping domains of items for the construction of tests or other indexes. For our purposes, the present application seemed appropriate and sufficient. In general, whether one pursues the logic of cluster analysis or of factor analysis, it seems to us that the goal of "most parsimonious description" gives the treatment of data a deceptive aura of mathematical rigor which they do not merit unless the communalities are extremely high. This is clearly evident in factor analysis, where higher communalities are generally associated with matrices of higher rank, i.e., a larger number of distinguishable dimensions. Relatively low communalities suggest to us that relevant variables are missing from the matrix, so that the true dimensions of the data are collapsed into a space that is of lower-dimensional order; this puts things together that do not really belong together. This introduces elements of arbitrariness into the analysis which are hidden behind the pseudoprecision of the technique. The issue is analogous to that of the number of significant digits with which data are reported; the rules of arithmetic, for instance, generally permit calculating statistics to an endless number of decimal places, but the quality of the data generally does not. Relatively crude data do not justify high-precision techniques. The cruder the data, the more we have to rely on good judgment for their analysis, rather than on mechanical rules of procedure; if the data are crude enough, they may not even justify that much.