APPENDIX C Meaning of Correlation Coefficients

The correlation coefficient is a measure of the degree of association between particular scores in one variable and particular scores in another when both sets of scores are expressed in the same standard units.

Suppose, for instance, that we wanted to measure the degree of association between height and weight. Experience would tell us that, on the average, taller people are also heavier, that is, height and weight are positively associated. But there are also some tall people who weigh less than some shorter people; the association is not perfect. But how far from perfection?
Height is measured in inches, and weight in pounds. If they were expressed in the same units, the question of how close the association between the two is would be relatively simple. If the association were perfect, then every person would have exactly the same height as weight. If the association were less than perfect, then at least some persons would have heights that differ from their weights, and, the greater the average difference, the less the correspondence between height and weight. But if, as just noted, height and weight are normally expressed in different units, we can still express them in the same units and thus be able to directly compare the heights and weights of persons, as follows:

(1) We subtract from the height of each individual the average height of the entire group, and, from each weight, the average weight. The scores are now expressed in what are called "deviational" units, but they are still in terms of, respectively, inches and pounds. If the average weight is 150 pounds, a person who weighs 160 has a deviational score of plus ten pounds, and a person who weighs 145 has a deviational score of minus five pounds. (2) We now relate the deviational scores to the respective variabilities of heights and of weights. Specifically, we divide each deviational score in height by the standard deviationl of the heights, and each deviational score in weight is divided by the standard deviation of the weights.

As a result of these transformations, we get two sets of scores which are directly comparable to each other. The units are no longer pounds and inches, but "standard deviations." For example, if the standard deviation of heights is 5 inches and the average height is 69 inches, then a person who is 65 inches tall has a standard score of —.80; that is, he is 8/10 of a standard deviation below the average height. If the average weight is 150 pounds, the standard deviation 10 pounds, and if the same person weighs 142 pounds, he has a standard score of —.80; that is, he is 8/10 of a standard deviation below the average weight. This means that, relative to the dispersions of heights and of weights, this person is exactly as far below the average height as he is below the average weight—a perfect correspondence, in this case. Another person might also have a standard score of —.80 in height, but a standard score of .20 in weight. This is a considerable discrepancy, as such scores go, and this person's standing with respect to weight is much higher than with respect to height.

When scores are expressed in the same units, we might, as suggested above, take the average of the differences between corresponding scores as a measure of the degree of association—the larger the average difference, the smaller the degree of association. For reasons that we cannot go into here, we take half the average of the squared differences instead of the average of the differences. Again, however, the larger this number, the smaller the degree of association. This number, it can be shown, cannot be larger than 2, and it obviously cannot be smaller than zero. It will, in fact, equal 2 when every score is of exactly the same magnitude as the score to which it is being compared, but reversed in sign, for instance, —.80 in height and +.80 in weight, +1.23 in height and —1.23 in weight, and so on. It will equal zero when all the corresponding scores are exactly alike. It will equal 1 when the standard scores in one variable are randomly associated with the scores in the other, that is, if there 'is absolutely no consistent trend for the standard scores in one variable to be like or different from the standard scores in the other.

In order to assign the highest possible degree of positive association (when all the differences equal zero) a value of +1.00 and the maximum possible degree of negative association (when all the corresponding scores are of the same magnitude but opposite in sign) a value of —1.00, we subtract half the average of the squared differences from 1. Perfectly random association will then have a value of zero. The result, somewhere betwen +1 and —1, is the coefficient of correlation.2 The important point to remember is that the correlation coefficient does not depend on the absolute values of the original scores but on the consistency of the relative standings of the cases with respect to the distributions of two variables.

As far as the degree of association goes, the sign of the correlation does not really matter. A correlation coefficient can always be reversed in sign without changing its numerical value, simply by turning one of the variables around. Thus, height and weight are positively correlated; by and large, taller people tend to be heavier and shorter people lighter. If we were to correlate shortness and weight, however, assigning higher scores to shorter people and lower scores to taller people, the correlation would be negative Similarly, if we were to correlate height and lightness, the correlation would be negative. But if we were to correlate shortness and lightness, the correlation would again be positive.

The sign of the correlation gives the direction of the relationship, as the variables are defined. If we have reason to be interested in the direction, then the sign of the correlation becomes important. Thus, if a hypothesis calls for a positive correlation, then a negative correlation is more disconfirming of that hypothesis than would be a zero correlation. There are occasions, however, when we have no special interest in the sign other than for orientation. In Chapter IV, for instance, we report on an inquiry into families of variables and, for such a purpose, the magnitudes of the correlations are of paramount importance.4

Correlation between Two-Valued Variables

Many variables can be measured along dimensions that, in principle, permit an infinite number of points if the precision of measurement is great enough; it is possible, however, to compute correlations for variables that permit as few as two possible points, e.g., the answers to an item on a test which may be scored zero or 1. When both variables are of this two-valued, or dichotomous, variety, the correlation coefficient we have described above is generally referred to as the phi coefficient or as the four-point correlation. The four-point correlation, however, suffers for certain purposes from the handicap that, if the over-all distributions of the two variables are not identical in shape, it is impossible to get correlations of +1.00 or —1.00; that is, the possible range of values is restricted.5 Hence, correlations obtained for differently distributed variables are not directly comparable.

Since, in Chapter IV, we deal with the correlations between two-valued variables, the particular device we have adopted to overcome the handicap should be explained. A many-valued variable can be rendered into a dichotomy by cutting it at some point. Thus, we can form two classes of heights, one consisting of persons who are less than, say, sixty-eight inches tall and the other of persons who are sixty-eight or more inches tall. Conversely, we can think of most dichotomies as the results of a cut in a many-valued variable. Thus, we can think of people who can give the right answer to a question as knowing more about the subject of that question than people who cannot answer the question correctly. A more finely graded test would make many distinctions among the people who answer the question correctly and, similarly, among those who answer it incorrectly. Moreover, whatever the shape of the many-valued distribution of scores, the scores can always be transformed in such a way that the distribution closely approximates the normal, or bell-shaped, distribution.6 A set of scores so treated is said to have been normalized.

If two dichotomies result from the cutting of two normal distributions, then, because of certain mathematical relationships involved, we can estimate from the joint distributions of the dichotomized variables what the correlation would have been if we had cross-tabulated the full sets of the original scores and computed the correlation therefrom. A correlation coefficient so estimated from the joint distribution of two dichotomies (i.e., on the assumption that each dichotomy represents a cut in a many-valued dimension in which the scores are normally distributed or in which the distributions have been normalized) is known as a tetrachoric correlation. The correlations among questionnaire items dealt with in Chapter IV were computed on this basis. Tetrachoric correlations have theoretical limits of +1 and —1 regardless of whether the two over-all distributions of the two-valued variables are identical.

Let us illustrate the idea of correlations among items with some hypothetical distributions. We shall consider two questionnaire items for purposes of the illustration.

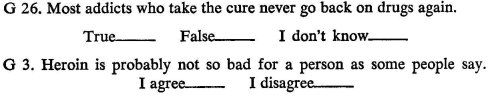
We shall treat these as two-valued variables. Giving the correct answer to the first and expressing what we take to be the desirable attitude toward the second are, respectively, the high-scoring responses; failing to give the correct answer to the first and expressing the undesirable attitude toward the second are, respectively, the low-scoring responses.

Let us consider a hypothetical distribution of the responses of 100 subjects to these two items:

Notice that about 86 per cent (31 out of 36) of those who give the correct answer to the first item disagree with the second, whereas about 55 per cent (35 out of 64) of those who do not give the correct answer to the first agree with the second. A total of sixty-six of the 100 subjects are either high-scoring or low-scoring on both items; only thirty-four score high on one but low on the other. In this instance, there is a positive correlation between giving the correct answer to the first and expressing a desirable attitude on the second. That is, there is a considerably higher probability of expressing the "right" attitude among subjects who give the correct answer than among those who do not. The calculated value of the tetrachoric correlation coefficient is approximately +.67.
Compare this outcome with the following hypothetical distribution:

In this case, the probability of expressing the "right" attitude is almost exactly the same (60 per cent) among those giving the correct answer as among those who do not. Just about half are consistently high or consistently low on both; about half are high on one, but low on the other. The correlation is about zero.

And consider, finally, the following hypothetical distribution:

In this case, 97 per cent of those giving the correct answer (35 out of 36) express the "wrong" attitude, whereas 92 per cent of those not giving the correct answer (59 out of 64) express the "right" attitude. Only six of the 100 respondents are consistently high or consistently low on both items; ninety-four are high on one, but low on the other. The correlation is negative, about —.98.

Note that, in all three illustrations, the marginals (i.e., the over-all distribution of each variable) are exactly the same. That is, 36 per cent of the total group of subjects give the correct answer to the first item, and 60 per cent express the "right" attitude. Obviously, if we were to consider only the marginal totals of the individual items, we would be neglecting fairly vital information. Note also that the over-all distribution of one variable differs from that of the other—a 36-64 break in the case of one, and a 40-60 break in the case of the other. This does not stop us from getting a tetrachoric correlation of virtually unity.

Interpreting a Correlation Coefficient

All that a correlation between two variables can tell us is that the corr'esponding scores tend to be associated in some way. It does not tell us why or how that correlation comes about. It may help to maintain perspective on correlation coefficients to indicate some of the ways in which substantial correlation can come about:

(1) Two variables may directly involve common components. With greater height, for instance, there are more of certain bones, flesh, and sinews; flesh, bones, and sinews, of course, contribute to weight. A high correlation between census-tract drug rates and delinquency rates would result if narcotics and other violations were committed only by socially alienated individuals and if such individuals always committed both types of offenses. It would follow that, the more socially alienated individuals in a census tract, the higher both rates would be; the socially alienated individuals would be common components of both rates.

(2) Two variables may be determined by a common cause. Assume, for instance, that poverty generates disrespect for social standards in a society that emphasizes economic success and plenty. Assume, further, that aggressive individuals with disrespect for social standards strike back in the form of criminal activity and that passive individuals with similar disrespect for social standards seek substitute, if illicit and illusory, gratification, such as that provided by drugs. Assume, finally, that each census tract is endowed with its fair share of highly aggressive and of highly passive individuals, although poverty is distributed in unequal proportions. In such a situation, there would be a high correlation between census-tract drug and delinquency rates, even though different individuals commit the two types of offense. The common cause is poverty.

(3) One variable may be in the causal sequence that leads to another. Assume, for instance, that illegal drugs are costly and that addicts must commit crimes to obtain the funds to buy drugs. Assume, further, that some census tracts have many more addicts than others. Such a state of affairs would lead to a high correlation between census-tract drug and delinquency rates. Drug use is a cause of delinquency. But, one may argue, delinquency existed before widespread drug use and cannot be caused by something that came after. Such an argument is commonly compelling. For instance, we note in Chapter III a high correlation between juvenile drug rate and poverty. Since the poverty rates were measured as of 1949, and since there were still very few juvenile users in 1949, it is absurd to think that juvenile drug use caused poverty—even if there were no other reasons for considering such a hypothesis untenable. The drug-rate–delinquency-rate example cannot, however, be so readily dismissed. It is conceivable that current delinquency is largely generated by drug use, i.e., that other causes of delinquency have virtually disappeared. This, for instance, is an inference (a not-logically-required inference, we must say) drawn by many from statistics that 60 per cent or more of the inmates of penal institutions are "drug addicts."
On the other hand, assume that people who are criminally inclined are attracted to narcotics precisely because they are illegal. In this event, we would also get a high correlation between drug and delinquency rates, but delinquency would be the cause of drug use. We report in Chapter V, that we found great difficulty in locating delinquents in the high-drug-rate areas who were not also drug-users. The assumption we are discussing might offer one explanation of such a finding.

(4) What may be interpreted as a special case of common components or of c6mmon cause—viz., correlated errors of measurement—may also bring about substantial correlation. Assume, for instance, that the true drug rates and delinquency rates are the same in all census tracts, but that the intensity of police activity varies markedly. This would produce a high correlation between the two obtained sets of rates, but each of the variables would actually be measuring intensity of police activity, the common component of the two measures, rather than what it purports to measure.

(5) The basis of the relationship may be complex, involving common components, common causes that tend to produce both effects independently, some reciprocal causation between the variables, and correlated errors—all operating at the same time.

(6) A real relationship, on whatever basis, between two variables may be masked by the operation of one or more additional variables. This point can be illustrated with the following hypothetical data. Assume that we have subdivided an area with 100,000 boys into 100 sections with 1,000 boys in each. Assume further that we have classified each section into the twenty-five sections with the highest poverty rates, the twenty-five sections with the next highest poverty rates, and so on. Similarly, assume that we have classified each section as one of the fifty highest in rates of change of residence or as one of the fifty lowest. Finally, assume that we have calculated drug rates, with the following results:

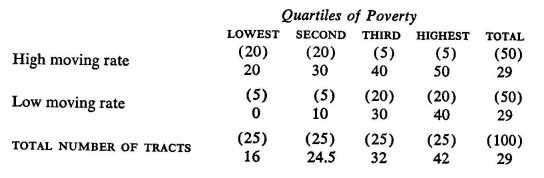
The numbers in parentheses designate the numbers of sections in each poverty-moving category. The other numbers designate the number of drug-involved cases per thousand boys. Observe that, at each poverty level, the drug rate for the sections in the high-moving-rate category is higher than for those in the low-moving-rate category. Yet, if we were simply to examine the relationship between drug rate and rates of changing residence without reference to poverty, the high- and the low-moving-rate sections have exactly the same drug rates. The relationship between moving rate and drug rate would be obscured by the relationship between moving rate and poverty.

Apart from the sheer fact of concomitant variation, a correlation coefficient is an ambiguous datum. It can only be interpreted in the light of additional information which heightens the credibility of one of the possible alternatives and lessens the credibility of others.

In the same manner, a high correlation between two questionnaire items, A and B, may be open to a variety of interpretations. Thus:

(1) A contributes directly to the causation or generation of B, or vice versa. In the first of the preceding hypothetical examples of a correlation between two items, we portrayed the high correlation between the awareness of the great difficulty of curing drug addiction and the feeling that heroin is indeed harmful in terms that suggested that the first is the cause of the second. But we could also interpret the correlation as follows: a strong feeling that heroin is harmful may dispose one to assume that addiction is difficult to cure, and skepticism about its harmfulness may dispose one to assume that addiction is readily curable. In other words, we could interpret the correlation by assuming that the answer to the second item tends to determine the answer to the first.

(2) A may generate a chain of events which lead to B, or vice versa. Thus, learning that, once an addict, always an addict, may conceivably sensitize one to other evidence of its undesirability, evoke unconscious complexes about incurable diseases (e.g., "wages of sin"), and so on, and it may be that these processes are the factors that lead to the conclusion that heroin is harmful.

(3) A and B may have no direct influence on each other, but each may be generated by the same set, or by correlated sets, of conditions. Thus, we might explain the correlation by assuming that the cultural atmosphere disposes one to answer the two items in a consistent manner, even though the two are never brought in apposition.

(4) A may be a component of B, or vice versa; A and B may contain common aspects or elements; or, under certain conditions, A may take on the coloration of B, or vice versa. Thus, "incurability" may be one of the meanings attributed to "harmfulness," or "harmfulness" one of the meanings attributed to "incurability." Or both items may have in common the fact that they offer an opportunity to express one's acceptance or rejection of the mores of society. Or, in an environment which is not overly hostile to the use of narcotics, ignorance may tend to robe itself in the garb of tolerance.

(5) All or some combination of the foregoing bases of relationship and possibly others as well may be simultaneously true. Thus, the relationship between the response tendencies evoked by the two items may be one of a vicious or beneficent circle; for example, ignorance of the facts about curability may produce, under certain conditions, a tolerant attitude which, in turn, may create a mental block toward learning the true facts and, hence, a rejection of the sources of authority which seek to propound the true facts; this rejection, in its turn, may cause one to lean over backward to be even more tolerant, and so forth. We could then conclude that the outlook on the cure of addiction tends to be shaped by an attitudinal, rather than an informational, current in the cultural atmosphere. The alternatives selected by individuals in responding to the addiction-cure item tend to be determined by where they stand with respect to the attitudinal complex or with respect to the forces that shape this complex.

This inherent ambiguity, from the viewpoint of causality, of described relationships between variables is not limited to the case where the relationship is expressed in the form of a correlation coefficient. That is, the ambiguity is not in the coefficient, but in the fact of correlation—of concomitant variation —itself, however such correlation may be described. We made our points, for example, about the "real" relationship (in the hypothetical illustration) between rates of changing residence and drug rates and about the masking of this relationship by the relationship between moving rate and poverty rate by displaying a table; we did not compute any correlation coefficients at all. In the same table, it is easy to see the existence of a relationship between drug rates and poverty rates even if one does not express the degree of relationship in a number or express the form of the relationship in a mathematical equation. 7 Whether or not we take the latter steps, the relationships themselves are subject to the varieties of interpretation that we have discussed with respect to the correlation coefficient. Does poverty, for instance, lead to drug use, or is there a factor that independently produces both?

Observed relationships have to be interpreted, and the interpretation has to be based on the additional information and the variety of alternative hypotheses that can be brought to bear on the issue. The process of interpretation requires judgment, and there is no alternative to this, short of direct experimentation.s One type of additional information that can be brought to bear on the interpretation of a relationship is to examine it in the context of a larger set of relationships. This does not eliminate the judgmental process; it simply increases the informational base in terms of which judgments are rendered. In Chapter III, we made use of correlation data to examine the contribution that individual variables can make to a statistical accounting of drug rates, by themselves and in combination with other variables. In Chapter IV, we make use of a network of correlations in a somewhat different fashion. There is no one variable on which we wish to focus to begin with; it is the network itself that is of primary interest to us.

The Correlation of Rates

We must here face an issue that has been touched on in an earlier footnote. Rates are tricky variables in correlational analysis. The issue may perhaps be made clear by an illustration due to Jerzy Neyman.s Neyman correlated birth rates with the number of storks in various counties of the United States and found a substantial correlation. The greater the number of storks, the greater, on the average, the birth rate. Before one takes this finding as support' for a certain theory of childbirth, however, one must note that it is a statistical artifact. Birth rate happens to be positively correlated with population size, the denominator used in computing birth rates. Storks, on the other hand, not indigenous to this country, tend to be found in zoos and menageries, which, in turn, tend to be located in highly populated areas, with the largest zoos in the most heavily populated areas. The correlation between birth rate and number of storks, it turns out, simply reflects the correlation between population size and number of storks; when a control is introduced for population size, the earlier correlation vanishes.

It should be obvious from this illustration that what has been called "spurious index correlation" is a special case of the more general proposition that correlation may arise between two variables as a result of their respective correlations with a third variable. The caveat expressed by many statisticians against spurious index correlation is a special case of the more general caveat against the possibility that a correlation between two variables is due to their respective associations with a—possibly unsuspected—third variable. The more general possibility does not bother us particularly. We do not correlate an index of poverty, for example, with drug rate because we suspect that poverty per se causes drug use. We know of no reason to suspect this as a possibility; quite the contrary, because illegal drugs are so terribly expensive. We carry out the correlation precisely because we suspect that poverty is associated with something that does stand in a causal relation to vulnerability to drug use. Whether that something is itself a cause or a consequence of poverty is, at the moment, of secondary importance.

We have already conceded that the most we can hope for from our analysis is a reasonable interpretation or a number of alternative reasonable interpretations, albeit interpretations based on established facts. Whether we interpret the "something" as cause, as consequence, or as incidental correlate of poverty depends on the plausibility of the hypotheses that might explain the obtained relationship between poverty and drug use. If our constructive imaginations have failed us in the interpretation of findings, we hope that some of our readers will be stimulated to come up with better interpretations or at least with alternative plausible interpretations that we may have failed to consider.

The possibility of spurious index correlation is, however, bothersome. The reason for the worry can be most readily explained by illustration. Suppose that drug rate is substantially correlated with number of adolescent boys, that percentage of income units earning $2,000 or less is substantially correlated with the number of units reporting on income, and that (as is likely to be the case, because both denominators are presumably substantially correlated with the size of the total population) the number of adolescent boys is substantially correlated with population size. Then the correlation between drug rate and this index of poverty could be, in whole or in part, the result of the respective correlations between each of the indexes and population size. This possibility, however—and it is one that is invited by the correlation of rates—is so remote from the thinking that leads us to investigate the correlation between the two indexes in the first place that we would not like to have to entertain it.

Fortunately, it turns out that the correlation between drug rate and number of adolescent boys within the groups of census tracts we are studying is just about zero. Hence, any correlation between drug rate and any of the other variables cannot have such a "spurious" basis.

We did not investigate the possibility of spurious index correlation among the other variables. The possibility is irrelevant, because we are not interested in explicating the causal contexts of the other variables." Moreover, in the case of these other variables, rates are precisely what we are interested in. Our assumption is that it is the relative incidence of, say, poverty that makes for a community climate hospitable to drug use.11

1 The standard deviation is the square root of the average of the squared deviational scores. Like the deviational scores, the standard deviation has the same dimension as the original scores. Thus, if the original scores are measured in inches, the standard deviation is measured in inches. To discuss why we take the standard deviation rather than the simple average of the deviations would involve us in technicalities that would take us too far afield. For present purposes, it is enough to note that the procedure involves the comparison of each deviational score to a deviation that may be said to be characteristic of the entire set of scores.

2 This account does not parallel the familiar versions of the product-moment correlation formula, but is algebraically identical to them and offers what seems to be the simplest explanation of what is involved. No one would, of course, actually compute a correlation coefficient in the manner described, except possibly for didactic purposes.

3 Such an inquiry is referred to as a cluster analysis, the idea of which is explained in Chapter IV and Appendix E. A cluster analysis was also, carried out on the variables dealt with in Chapter III. We have not, however, reported this analysis, because it does not materially add to or subtract from the story we have told. The definable clusters vary somewhat from borough to borough, but this is related to a point we deal with in the chapter, viz., that some of the variables do not have consistent meanings in the three boroughs in terms of their patterns of relationships with the other variables. The point is of special significance only in relation to general studies of urban ecology and in inspiring caution with the apparent face validity of many ecological variables.
For the same reason, we have not reported the beta coefficients in the multiple correlation analysis. As might be expected, the highest betas in each borough represent all the clusters and, in Manhattan and the Bronx, some of the variables that stand off by themselves, e.g., the percentage excess of adolescent females over males. Such a scattering of betas lends emphasis to our final point in the chapter that no one group of unwholesome factors can be said to be exclusively associated with the vulnerability of neighborhoods to the use of narcotics by juveniles. The prepotency of the economic factor again shows up in the fact that, in Manhattan and Brooklyn, poverty (i.e., percentage of units with incomes of $2,000 or less) has the highest beta—twenty-five times as large as the smallest in Manhattan and twelve times as large as the smallest in Brooklyn; in the Bronx, this variable has a relative weight of twenty-six, but is exceeded by two of the more ambiguous variables (percentage of families living at a new address and number of employees per resident, the latter with a negative beta). The betas were computed only for the multiple regression equation involving all the variables but percentage of Negroes and percentage of Puerto Ricans.

4 The signs enter also, but there is no special interest in the sign of the correlation between any pair of variables other than in determining sets of variables that stand in a special kind of relationship to one another. Variables are freely reflected (turned over) in order to minimize the number of negative signs, a process that makes it easier to find such sets.

5 In principle, the same limitation applies to the general case; it has less material consequence, however, as the number of distinguished points in each variable rises. If 100 people answer two items, and, say, fifty answer the first correctly and only twenty answer the second correctly, then, scoring each item zero for an incorrect and 1 for a correct answer, the average on the first item is .5 and, on the second, .2. For the first item, there are fifty people with deviational scores of +.5 and fifty with —.5; the standard deviation is .5. For the second item, there are twenty people with deviational scores of +.8, and eighty with —.2; the standard deviation is .4. Hence, for the first item, there are fifty cases with standard scores of +1, and fifty with —1. By contrast, for the second item, there are twenty with standard scores of +2, and eighty with —.5. Even if all the people who gave the right answer to the second item also answered the first item correctly, each of them would have one standard score of +1 and one of +2, and the difference obviously does not equal zero. Similarly, if all the people who got the first answer wrong also gave the wrong answer to the second, they would have standard scores of —1 and —.5, and, again the difference does not equal zero. So, even for the people with perfectly matching performances (right on both items or wrong on both items), we do not get perfectly matching standard scores; and, with one item breaking 50-50 and the other 20-80, it is impossible not to get cases without matching performances. The highest possible positive four-point correlation in this instance is .50; the most extreme negative four-point correlation possible is —.50.

6 The normal distribution has the following distinctive properties: there is a piling-up of cases around the average; as one moves in either direction from the average, the number of cases falls off; between the average and any given point above it, there is the same number of cases as between the average and a point equally distant below it; 34 per cent of the cases are found between the average and a point one standard deviation above it, and a like proportion of cases, between the average and a point one standard deviation below it; 47.7 per cent of the cases are found between the average and a point two standard deviations away from it, 49.87 per cent of the cases between the average and a point three standard deviations away, etc. The normal distribution is a common one in nature, and it often, but not always, makes sense to assume that, if the obtained distribution is not normal, the fault is in the measuring instrument, rather than in the true distribution. In such cases, the scores are commonly normalized. The IQ's, for instance, determined by one of the most commonly used intelligence tests are based on normalized, rather than directly obtained, scores.

7 To the student of statistics, this is apt to be one of the most familiar properties of the correlation coefficient; it is the essential term in the equation of a straight line. If both variables are expressed as standard scores, this equation is Z1(2) —    Z 1(2) - 12 2,
where Zi(2) designates the "expected" score in Variable 1 that corresponds to a particular standard score in Variable 2, z2 designates standard scores in Variable 2, and r12 is the coefficient of correlation between the two variables. Hence, the correlation coefficient describes a relationship which has the form of a straight line. The "expected" score z1(2) that corresponds to a particular z2 is an approximation of the actual average score on Variable 1 that is obtained by the individuals who earn that particular score on Variable 2. If we were to compute a series of such actual averages on Variable 1 for each of the scores on Variable 2 and if these averages did not tend to fall along a straight line, the relationship would be said to be curvilinear; in such an event, the correlation coefficient we have described would underestimate the true degree of relationship, sometimes quite markedly so.

8 This point is discussed in the text of Chapter III.

9 J. Neyman, Lectures and Conferences on Mathematical Statistics and Probability (2nd ed.; Washington: Graduate School, U.S. Department of Agriculture, 1952).

10 It should be pointed out that spurious index correlation between these variables would make for a higher common factor variance than would be found if some procedure other than the computation of rates were used to control for the respective sizes of the base populations. The procedure suggested by Neyman is to partial out the population. Thus, if drug rate had been substantially correlated• with male adolescent population, an alternative to drug rate would have been the number of drug-involved cases minus the number to be expected on the basis of the correlation between the number of cases and the number of adolescent boys. If there were a substantial curvilinear component in the latter correlation, the procedure would be more complicated, but the same in principle. The same procedure would, of course, be followed for all indexes involving a relative-to-thepopulation aspect.

11 Our assumption is that the relative incidence of poverty is more easily discernible as a rate than through some complicated statistical inference based on the relation between number of impoverished families and another variable—population size. By placing the advantage on the side of discernibility, we think that we have increased the likelihood that the "something" linking poverty and drug rate is in the causal sequence between the two, rather than in the causal sequence leading to poverty. The alternative procedure mentioned in Note 10 would, we think, give less emphasis to the psychological aspect of poverty, as it would to the other variables.