APPENDIX A
Calculation of Drug Rates

The Early Period

Drug rates for the forty-six–month "early period," which began on January 1, 1949, were computed on the assumption that the number of males sixteen to twenty for a given geographic area remained constant over this periodmove-outs being compensated for by move-ins and boys growing out of the age group being compensated for by boys growing into it—and equaled the number reported by the 1950 census for the fifteen-to-nineteen age bracket (i.e., sixteen to twenty in 1951). Drug rates were calculated in terms of the number of drug cases per one thousand males counted by the census in this age range. A drug rate of fifty would therefore mean that, for every thousand boys between sixteen and twenty years old in 1950, fifty drug-connected cases in that age bracket at the time of discovery came to official attention during the forty-six–month period. The reader should note that this does not mean that 5 per cent of the boys living in the area at one time or another and in the designated age range for at least part of the period became drug cases during the period with which we were concerned, since each year sees additional youngsters coming into the age bracket and others growing out of it. Our base unit was a hypothetical boy living in the area and in the age bracket for the full forty-six months. Such a unit might, for example, be made up of two actual boys, one meeting the qualifications for fourteen months and the second for thirty-two months. The reported drug rates should be interpreted as indexes of narcotics activity which helped us compare the relative incidence of new cases from neighborhood to neighborhood.

A more refined method of calculating rates was also tested. It took into account the number of new cases each year and the eligible population for that year, still, however, making the necessary assumption that move-outs were balanced by move-ins. Thus, for 1951, the rate was calculated as

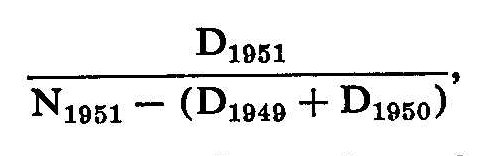
where D1949, D1950, and D1951 are the numbers of new cases for the designated years and N1951 refers to the number of boys in the fifteen-to-nineteen age range at the time of the census (i.e., in the sixteen-to-twenty age range in 1951). The reason for subtracting D1949 and D1950 from N1951 is that these cases are no longer part of the eligible population. Similar rates were computed for each year of the period (with an adjustment for the number of cases in 1952).1 The over-all rate was obtained by adding the yearly rate and multiplying by 1,000. After calculating rates both ways for twenty-three census tracts, it became obvious that the two methods were yielding virtually identical results (the correlation was .996), and the simpler method was adopted.

The rates were computed for a forty-six—month period. The reader who prefers to see rates on a yearly basis should multiply the cited figures by 12/46, or .26. Such an adjustment would have no effect on the comparisons made.

The Later Period

As we get further away from the year of the census, the census figures become less dependable. It was consequently necessary to prepare revised estimates of the number of males in our age bracket who resided in a given area. Since we could get data relevant to such estimates only on a health-area basis, drug rates for the later period were computed only for health areas.

THE NUMERATOR

The period of observation for the later period was thirty-six months, beginning November 1, 1952, in comparison to the forty-six—month earlier period. In order to make the rates comparable to those of the earlier period, the number of drug-involved cases in each health area was multiplied by 46/S6; the resulting numbers were used as the numerators in computing drug rates. Although the numbers for the early and late periods were thus comparable, errors of measurement (i.e., enumeration errors) must be of relatively greater magnitude for the later period. It should also be remembered that we have greater confidence in the comprehensiveness of the case-finding procedures in the early period; this, too, would affect the accuracy of the rates.

THE DENOMINATOR

Three separate estimates were made of the number of males in the sixteento-twenty age bracket in each health area; two of these were for the base year 1954, and one for the year 1955. Drug rates were computed on the basis of each estimate. The logic of the three estimates was the same; only the data utilized were different. It was assumed that the number of males in our age bracket in a given health area would increase or decrease relative to the 1950 figures in proportion to the increase or decrease in the total population. Thus,

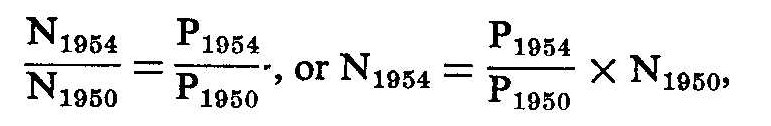
where N1954 is the number of males in the indicated age bracket in 1954, N1950 is the number of males aged twelve to sixteen in 1950 (these are, of course, the ones who were in the age range sixteen to twenty in 1954), P1954 1954
is the total population in 1950, and P1950 the total population of the health area in 1950.

We assumed that the number of births (or, alternatively, deaths or, again alternatively, dwelling units) for a given year was directly proportional to the size of the total population. That is,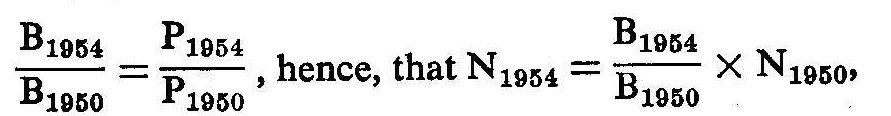

where B1954 and B1950 are the number of births in a health area in, respectively, 1954 and 1950. Similarly with regard to the number of deaths and the number of occupied dwelling units. Since additional information was available in connection with the birth and death data, the actual calculations were somewhat more complicated. All these data were made available to us through the cooperation of the Department of Planning of the City of New York.

Estimate Based on Birth Data. We had or could calculate the number of births in 1954, in each health area, to white mothers who were themselves born in Puerto Rico, to nonwhite mothers from Puerto Rico, to other white mothers, and to other nonwhite mothers. This suggested the possibility of estimating the numbers of males aged sixteen to twenty in each of these four groups. For 1950, however, we did not have precisely parallel information and, consequently, had to estimate it. We did have the 1950 health-area figures for numbers of births to all white and nonwhite mothers; and we had the 1950 totals, by borough, for each of the four groups.

For each borough, we divided the number of births to white Puerto Rican mothers by the total number of white Puerto Ricans. Multiplying this ratio by the number of white Puerto Ricans in a given health area gave us an estimated number of births to white Puerto Rican mothers in that health area in 1950; and so on for each health area. For each health area, we now subtracted this estimate from the number of births to all white mothers, in order to get an estimate of the number of births to non-Puerto Rican white mothers. A similar procedure gave us estimates for each health area of the number of births to nonwhite Puerto Rican mothers and of the number of births to the other nonwhite mothers.

Finally, we had to estimate for the individual health areas the numbers of boys in the twelve-to-sixteen age range in each of the four groups in 1950. We computed the ratio of the number of white Puerto Rican boys in the twelve-to-sixteen group to the total number of white Puerto Ricans in the city2 and multiplied it by the number of white Puerto Ricans in the health area. Subtracting this estimate from the total number of white boys in this age range gave us an estimate of the number of white non-Puerto Rican boys in the desired age range. A similar procedure gave us estimates of the numbers of nonwhite Puerto Ricans and of other nonwhites in each health area.

We now had, for each of the subgroups, actual counts of the numbers of births in 1954 and parallel estimates of the number of births in 1950; and We had estimates of the number of boys in the twelve-to-sixteen bracket in 1950. We could, therefore, from the basic formula described above, estimate, for each health area, the number of boys in each of the subgroups in the sixteento-twenty bracket in 1954. Totaling the estimates for the four subgroups gave us our estimate of the total number of boys in the sixteen-to-twenty bracket in each health area in 1954.

Estimate Based on Death Data. We had, for each health area, the numbers of deaths among whites and nonwhites in 1954. We had parallel information for 1950. We also had, for each health area, the number of whites and the number of nonwhites in the twelve-to-sixteen age group in 1950. That is, we had all the data necessary to estimate, on the basis of the death data, the numbers of white and nonwhite boys in each health area in 1954; all that was necessary was to substitute in the basic formula. Adding the two estimates gave us the desired estimate of the total number of boys in the sixteen-totwenty bracket in each health area in 1954.

Estimate Based on Occupied Dwelling Units. The Sanborn Map Coppany made a count of the number of occupied dwelling units in each health area in late 1955. We had parallel information and also the total number of boys in the twelve-to-sixteen bracket for each health area from the 1950 census. Substituting in the basic formula gave us our third estimate of the total number of boys in the sixteen-to-twenty bracket in each health area in 1954.

COMPARABILITY OF DRUG RATES

The three procedures for estimating the denominators for computing the health-area drug rates were so different from one another and the data utilized were also so different, that it became desirable to check on the consistency of the results obtained by the various methods.

In our maps of the distribution of drug rates in the early period, we had distinguished seven levels of drug rates. We accordingly classified each of the drug rates for the later period obtained by each of the estimating procedures into these seven levels. We then computed Robinson's coefficient of agree-menta to measure the concordance among the three methods in terms of the way each method would classify an area into one of the seven class intervals used on our maps. For the 265 health areas with which we are concerned, the Robinson measure indicated that the three methods would yield virtually identical drug-rate maps. The coefficient of agreement between the system based on births and that based on deaths was .98; between the birth system and the dwelling-unit system, .99; and, finally, between the death system and the dwelling-unit system, .98.

These high degrees of agreement should not engender false optimism. Basically, they mean that estimates of the population totals obtained by the three methods should be highly consistent. It should be remembered, however, that a health-area drug rate computed by each of the methods involves the same adjusted numerator, and the denominator involves the same assumptions in the basic formula, e.g., the constancy over time of the proportion of the age cohort to the total population in each health area. In other words, there are possible sources of error common to the three procedures. On the other hand, the basic formula was applied in such differing ways in calculating the three denominators (to three subgroups separately in the birth-data method, to two in the death-data method, and to the total group in the dwelling-unit method) that the common assumptions involved in calculating the denominators would have been severely strained if they were not at least approximately correct.

Final Estimates of Later-Period Drug Rates. The later-period drug rates used in the final analysis—i.e., in the correlations with the early-period drug rates—were simple averages of the three estimates. This would tend to average out variable errors in the three estimates. It would not, of course, get rid of common errors.

STATISTICAL FOOTNOTES

a W. W. Robinson, "The Statistical Measure of Agreement," American Sociological Review, 22 (1957), 17-25. Robinson's measure of agreement is a variant of the intraclass correlation coefficient, itself a variant of the familiar Pearson product-moment correlation which we have used elsewhere. Unlike the usual product-moment correlation, the intraclass correlation is sensitive to absolute, rather than simply relative, discrepancies between two sets of scores.

1 At the time these rates were calculated, we did not have the data on cases detected during the last two months of 1952. This also accounts for the forty-six-month period referred to in connection with the method of computing rates.

2 Actually, this also involved an estimate. The census tabulation did not give the number of white Puerto Rican boys in the twelve-to-sixteen age group; it gave the total for the ten-to-eighteen range. We estimated the number who were twelve-to-sixteen years old by halving the latter number.